Recurso original - Geeks for Geeks | (Version - Junio 1, 2023)

Algoritmo Ford-Fulkerson para el problema de flujo máximo

El algoritmo de Ford-Fulkerson es un algoritmo ampliamente utilizado para resolver el problema de flujo máximo en una red de flujo. El problema de flujo máximo implica determinar la cantidad máxima de flujo que se puede enviar desde un vértice fuente a un vértice sumidero en un grafo dirigido y ponderado, sujeto a las restricciones de capacidad en las aristas.

El algoritmo funciona encontrando iterativamente un camino aumentante, que es un camino desde la fuente hasta el sumidero en el grafo residual, es decir, el grafo obtenido al restar el flujo actual de la capacidad de cada arista. El algoritmo luego incrementa el flujo a lo largo de este camino en la cantidad máxima posible, que es la capacidad mínima de las aristas a lo largo del camino.

Problema:

Dado un grafo que representa una red de flujo donde cada arista tiene una capacidad. Además, dados dos vértices, la fuente ‘s’ y el sumidero ‘t’ en el grafo, encuentra el flujo máximo posible de ‘s’ a ‘t’ con las siguientes restricciones:

• El flujo en una arista no excede la capacidad dada de la arista.
• El flujo entrante es igual al flujo saliente para cada vértice, excepto ‘s’ y ‘t’.

Por ejemplo, considera el siguiente grafo del libro CLRS.

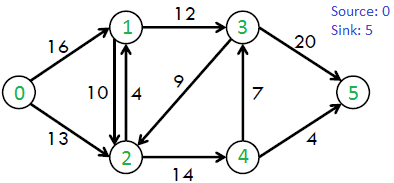
El flujo máximo posible en el gráfico anterior es 23.

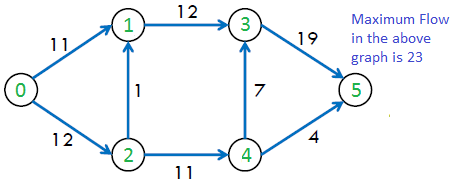
Algoritmo de Ford-Fulkerson

La idea básica del algoritmo de Ford-Fulkerson es la siguiente:

1. Inicializar con un flujo inicial de 0.
2. Mientras exista un camino aumentante desde la fuente hasta el sumidero:
   - Encontrar un camino aumentante usando cualquier algoritmo de búsqueda de caminos, como búsqueda 
     en anchura (BFS) o búsqueda en profundidad (DFS).
   - Determinar la cantidad de flujo que se puede enviar a lo largo del camino aumentante, que es la 
     capacidad residual mínima a lo largo de las aristas del camino.
   - Incrementar el flujo a lo largo del camino aumentante por la cantidad determinada.
3. Devolver el flujo máximo.

Complejidad temporal: La complejidad temporal del algoritmo anterior es O(max_flow * E). Ejecutamos un bucle mientras exista un camino aumentante. En el peor de los casos, podemos agregar 1 unidad de flujo en cada iteración. Por lo tanto, la complejidad temporal se convierte en O(max_flow * E).

¿Cómo implementar el algoritmo simple anterior? Primero definamos el concepto de grafo residual, que es necesario para entender la implementación.

El grafo residual de una red de flujo es un grafo que indica el flujo adicional posible. Si hay un camino desde la fuente al sumidero en el grafo residual, entonces es posible agregar flujo. Cada arista de un grafo residual tiene un valor llamado capacidad residual, que es igual a la capacidad original de la arista menos el flujo actual. La capacidad residual es básicamente la capacidad actual de la arista.

Hablemos ahora de los detalles de implementación. La capacidad residual es 0 si no hay una arista entre dos vértices del grafo residual. Podemos inicializar el grafo residual como el grafo original ya que no hay flujo inicial y, inicialmente, la capacidad residual es igual a la capacidad original. Para encontrar un camino aumentante, podemos hacer un BFS o DFS del grafo residual. Hemos usado BFS en la implementación a continuación. Usando BFS, podemos averiguar si hay un camino desde la fuente al sumidero. BFS también construye el array parent[]. Usando el array parent[], recorremos el camino encontrado y encontramos el flujo posible a través de este camino encontrando la capacidad residual mínima a lo largo del camino. Luego agregamos el flujo del camino encontrado al flujo total.

Lo importante es que necesitamos actualizar las capacidades residuales en el grafo residual. Restamos el flujo del camino de todas las aristas a lo largo del camino y agregamos el flujo del camino a lo largo de las aristas inversas. Necesitamos agregar el flujo del camino a lo largo de las aristas inversas porque puede ser necesario enviar flujo en dirección inversa más tarde (ver el siguiente enlace para un ejemplo). https://www.geeksforgeeks.org/max-flow-problem-introduction/