Recurso original - Programiz
Algoritmo Ford-Fulkerson
El algoritmo de Ford-Fulkerson es un enfoque voraz para calcular el flujo máximo posible en una red o un grafo.
Se usa el término “red de flujo” para describir una red de vértices y aristas con una fuente (S) y un sumidero (T). Cada vértice, excepto S y T, puede recibir y enviar una cantidad igual de material a través de él. S solo puede enviar y T solo puede recibir material.
Podemos visualizar la comprensión del algoritmo utilizando un flujo de líquido dentro de una red de tuberías de diferentes capacidades. Cada tubería tiene una cierta capacidad de líquido que puede transferir en un instante. Para este algoritmo, vamos a encontrar cuánta cantidad de líquido puede fluir desde la fuente hasta el sumidero en un instante usando la red.
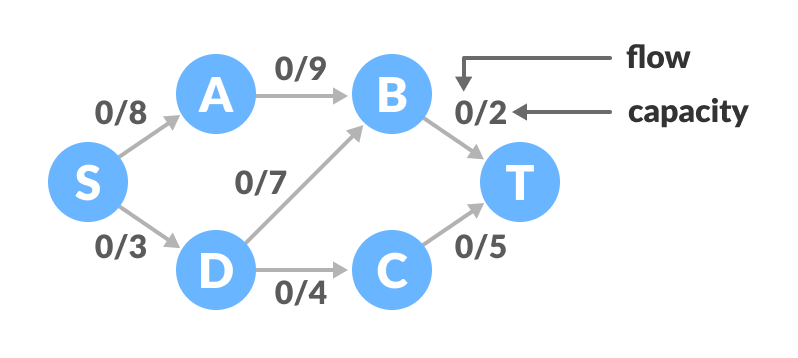
Terminología Utilizada
Camino Aumentante
Es el camino disponible en una red de flujo.
Grafo Residual
Representa la red de flujo que tiene flujo adicional posible.
Capacidad Residual
Es la capacidad de la arista después de restar el flujo de la capacidad máxima.
¿Cómo funciona el algoritmo de Ford-Fulkerson?
El algoritmo sigue los siguientes pasos:
- Inicializar el flujo en todas las aristas a 0.
- Mientras haya un camino aumentante entre la fuente y el sumidero, agregar este camino al flujo.
- Actualizar el grafo residual.
También podemos considerar el camino inverso si es necesario, porque si no los consideramos, puede
que nunca encontremos un flujo máximo.Los conceptos anteriores se pueden entender con el siguiente ejemplo.
Ejemplo de Ford-Fulkerson
Al inicio, el flujo de todas las aristas es 0.
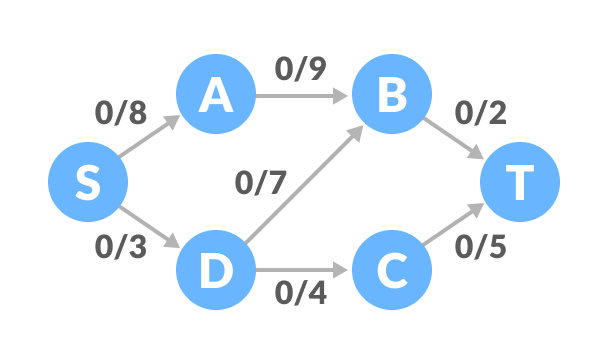
- Seleccionemos un camino arbitrario de S a T. En este paso, seleccionamos el camino
S-A-B-T.

La capacidad mínima entre las tres aristas es 2 (B-T). Basándonos en esto, actualizaremos el flujo/capacidad para cada arista del camino.

- Selecciona otro camino
S-D-C-T. La capacidad mínima entre estas aristas es 3 (S-D).

Actualiza las capacidades según esto.

- Ahora, consideremos también el camino inverso
B-D. Seleccionando el caminoS-A-B-D-C-T. La capacidad residual mínima entre las aristas es 1 (D-C).

Actualizando las capacidades.

Se consideran por separado las capacidades para los caminos directos e inversos.
- Sumando todos los flujos = 2 + 3 + 1 = 6, que es el flujo máximo posible en la red de flujo.
Nota que si la capacidad de cualquier arista está llena, entonces ese camino no se puede utilizar.
Aplicaciones del algoritmo de Ford-Fulkerson:
- Distribución de tuberías de agua
- Problema de emparejamiento bipartito
- Circulación con demandas