Recurso original - Geeks for Geeks | (Version - Septiembre 11, 2023)

Codificación Huffman

La codificación Huffman es un algoritmo de compresión de datos sin pérdidas. La idea es asignar códigos de longitud variable a los caracteres de entrada, donde las longitudes de los códigos asignados se basan en las frecuencias de los caracteres correspondientes.

Los códigos de longitud variable asignados a los caracteres de entrada son códigos prefijos, lo que significa que los códigos (secuencias de bits) se asignan de tal manera que el código asignado a un carácter no es el prefijo del código asignado a ningún otro carácter. De esta manera, la Codificación Huffman asegura que no haya ambigüedad al decodificar la secuencia de bits generada.

Veamos un ejemplo contrario para entender los códigos prefijos. Supongamos que hay cuatro caracteres: a, b, c y d, y sus códigos de longitud variable correspondientes son 00, 01, 0 y 1. Esta codificación lleva a ambigüedad porque el código asignado a c es el prefijo de los códigos asignados a a y b. Si la secuencia de bits comprimida es 0001, la salida descomprimida puede ser “cccd”, “ccb”, “acd” o “ab”.

Consulta esto para aplicaciones de la Codificación Huffman.

Hay principalmente dos partes principales en la Codificación Huffman:

Construir un árbol de Huffman a partir de los caracteres de entrada.
Recorrer el árbol de Huffman y asignar códigos a los caracteres.

Algoritmo

El método que se utiliza para construir un código de prefijo óptimo se llama codificación Huffman.

Este algoritmo construye un árbol de abajo hacia arriba. Podemos denotar este árbol como T.

Sea |c| el número de hojas.

|c| -1 son el número de operaciones requeridas para fusionar los nodos. Q es la cola de prioridad que se puede usar mientras se construye el montículo binario.

Algorithm Huffman (c)
{
   n= |c| 

   Q = c 
   for i<-1 to n-1

   do
   {

       temp <- get node ()

      left (temp] Get_min (Q) right [temp] Get Min (Q)

      a = left [templ b = right [temp]

      F [temp]<- f[a] + [b]

      insert (Q, temp)

    }

return Get_min (0)
}

Pasos para construir un árbol de Huffman

La entrada es una matriz de caracteres únicos junto con su frecuencia de ocurrencias y la salida es el árbol de Huffman.

Crea un nodo hoja para cada carácter único y construye un montículo mínimo de todos los nodos hoja (el montículo mínimo se utiliza como una cola de prioridad. El valor del campo de frecuencia se utiliza para comparar dos nodos en el montículo mínimo. Inicialmente, el carácter menos frecuente está en la raíz).
Extrae dos nodos con la frecuencia mínima del montículo mínimo.
Crea un nuevo nodo interno con una frecuencia igual a la suma de las frecuencias de los dos nodos. Haz que el primer nodo extraído sea su hijo izquierdo y el otro nodo extraído sea su hijo derecho. Agrega este nodo al montículo mínimo.
Repite los pasos #2 y #3 hasta que el montículo contenga solo un nodo. El nodo restante es el nodo raíz y el árbol está completo.

Entendamos el algoritmo con un ejemplo:

character	Frequency
a	5
b	9
c	12
d	13
e	16
f	45

Paso 1: Construye un montículo mínimo que contiene 6 nodos donde cada nodo representa la raíz de un árbol con un solo nodo. Paso 2: Extrae dos nodos de frecuencia mínima del montículo mínimo. Agrega un nuevo nodo interno con frecuencia 5 + 9 = 14.

Ilustración paso 2

Ahora el montículo mínimo contiene 5 nodos donde 4 nodos son raíces de árboles con un solo elemento cada uno, y un nodo del montículo es raíz de un árbol con 3 elementos.

character	Frequency
c	12
d	13
Internal Node	14
e	16
f	45

Paso 3: Extraer dos nodos de frecuencia mínima del montículo. Agregar un nuevo nodo interno con frecuencia 12 + 13 = 25.

Ilustración paso 3

Ahora el montículo mínimo contiene 4 nodos donde 2 nodos son raíces de árboles con un solo elemento cada uno, y dos nodos del montículo son raíces de árboles con más de un nodo.

character	Frequency
Internal Node	14
e	16
Internal Node	25
f	45

Paso 4: Extraer dos nodos de frecuencia mínima. Agregar un nuevo nodo interno con frecuencia 14 + 16 = 30.

Ilustración paso 4

Ahora el montículo mínimo contiene 3 nodos.

character	Frequency
Internal Node	25
Internal Node	30
f	45

Paso 5: Extraer dos nodos de frecuencia mínima. Agregar un nuevo nodo interno con frecuencia 25 + 30 = 55.

Ilustración paso 5

Ahora el montículo mínimo contiene 2 nodos.

character	Frequency
f	45
Internal Node	55

Paso 6: Extraer dos nodos de frecuencia mínima. Agregar un nuevo nodo interno con frecuencia 45 + 55 = 100.

Ilustración paso 6

Ahora el montículo mínimo contiene solo un nodo.

Dado que el montículo contiene solo un nodo, el algoritmo se detiene aquí.

Pasos para imprimir los códigos del árbol de Huffman

Recorre el árbol formado comenzando desde la raíz. Mantén un arreglo auxiliar. Mientras te muevas hacia el hijo izquierdo, escribe 0 en el arreglo. Mientras te muevas hacia el hijo derecho, escribe 1 en el arreglo. Imprime el arreglo cuando se encuentre un nodo hoja.

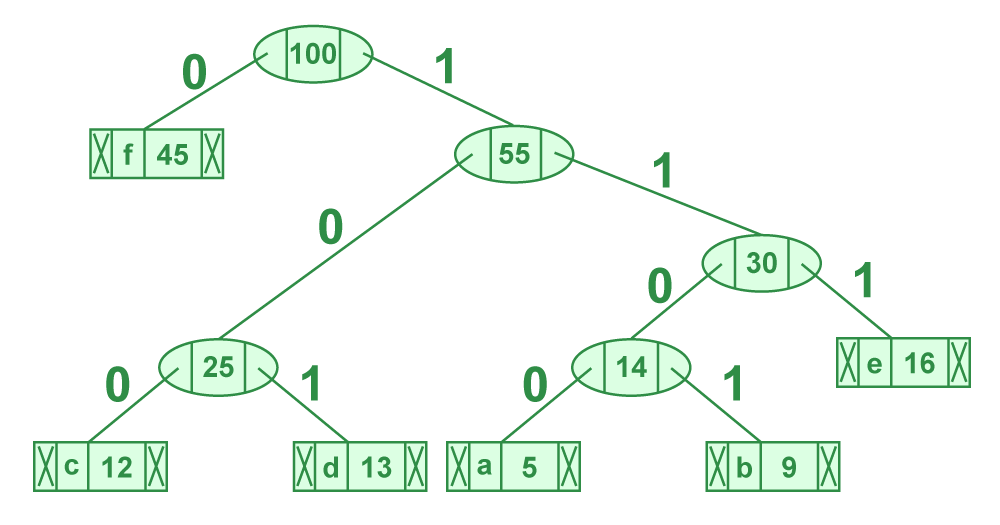
Pasos para imprimir el código

Los códigos son los siguientes:

character	code-word
f	0
c	100
d	101
a	1100
b	1101
e	111

Implementación

A continuación se muestra la implementación del enfoque anterior en Python3.

# A Huffman Tree Node 
import heapq 


class node: 
	def __init__(self, freq, symbol, left=None, right=None): 
		# frequency of symbol 
		self.freq = freq 

		# symbol name (character) 
		self.symbol = symbol 

		# node left of current node 
		self.left = left 

		# node right of current node 
		self.right = right 

		# tree direction (0/1) 
		self.huff = '' 

	def __lt__(self, nxt): 
		return self.freq < nxt.freq 


# utility function to print huffman 
# codes for all symbols in the newly 
# created Huffman tree 
def printNodes(node, val=''): 

	# huffman code for current node 
	newVal = val + str(node.huff) 

	# if node is not an edge node 
	# then traverse inside it 
	if(node.left): 
		printNodes(node.left, newVal) 
	if(node.right): 
		printNodes(node.right, newVal) 

		# if node is edge node then 
		# display its huffman code 
	if(not node.left and not node.right): 
		print(f"{node.symbol} -> {newVal}") 


# characters for huffman tree 
chars = ['a', 'b', 'c', 'd', 'e', 'f'] 

# frequency of characters 
freq = [5, 9, 12, 13, 16, 45] 

# list containing unused nodes 
nodes = [] 

# converting characters and frequencies 
# into huffman tree nodes 
for x in range(len(chars)): 
	heapq.heappush(nodes, node(freq[x], chars[x])) 

while len(nodes) > 1: 

	# sort all the nodes in ascending order 
	# based on their frequency 
	left = heapq.heappop(nodes) 
	right = heapq.heappop(nodes) 

	# assign directional value to these nodes 
	left.huff = 0
	right.huff = 1

	# combine the 2 smallest nodes to create 
	# new node as their parent 
	newNode = node(left.freq+right.freq, left.symbol+right.symbol, left, right) 

	heapq.heappush(nodes, newNode) 

# Huffman Tree is ready! 
printNodes(nodes[0])

Salidas

f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111

Complejidad temporal: O(nlogn) donde n es el número de caracteres únicos. Si hay n nodos, extractMin() se llama 2*(n – 1) veces. extractMin() toma O(logn) tiempo ya que llama a minHeapify(). Entonces, la complejidad general es O(nlogn). Si el arreglo de entrada está ordenado, existe un algoritmo de tiempo lineal. Pronto discutiremos esto en nuestra próxima publicación.

Complejidad espacial: O(N)

Aplicaciones de la Codificación Huffman:

Se utilizan para transmitir faxes y texto.
Son utilizados por formatos de compresión convencionales como PKZIP, GZIP, etc.
Los códecs multimedia como JPEG, PNG y MP3 utilizan codificación Huffman (para ser más precisos, los códigos de prefijo). Es útil en casos donde hay una serie de caracteres que ocurren con frecuencia.