Aprendiendo Desarrollo

Estructuras de datos

Como su nombre indica, una Estructura de Datos es una forma de organizar los datos en la memoria para que puedan utilizarse de manera eficiente. Algunas estructuras de datos comunes incluyen arrays, listas enlazadas, pilas, tablas hash, colas, árboles, montículos y grafos.

¿Por qué necesitamos Estructuras de Datos?

Así como las estructuras de datos son usadas para almacenar datos de una forma organizada, y dado que los datos son la entidad más crucial en informática, el verdadero valor de las estructuras de datos es claro.

No importa qué problema estés resolviendo, de un modo u otro tienes que tratar con datos — ya sea el salario de un empleado, precios de acciones, una lista de compras, o incluso un directorio telefónico simple.

Basado en diferentes escenarios, los datos necesitan ser almacenados en un formato específico. Tenemos un puñado de estructuras de datos que cubren nuestra necesidad de almacenar datos en distintos formatos.

Arrays

Los arrays almacenan elementos en ubicaciones de memoria contiguas, lo que resulta en direcciones fácilmente calculables para los elementos almacenados, y esto permite un acceso más rápido a un elemento en un índice específico.

Aquí te muestro cómo se implementa un array en JavaScript:

let miArray = [1, 2, 3, 4, 5]; // Este es un array de números
console.log(miArray[0]); // Imprime el primer elemento del array: 1

Y aquí en Python:

mi_lista = [1, 2, 3, 4, 5] # Esta es una lista, el equivalente a un array en Python
print(mi_lista[0]) # Imprime el primer elemento de la lista: 1

Los arrays se utilizan en una gran variedad de aplicaciones. Algunos ejemplos incluyen:

  • Almacenar datos: Si tienes un conjunto de elementos del mismo tipo, puedes almacenarlos en un array en lugar de declarar variables individuales para cada uno de ellos.
  • Acceso rápido a los datos: Los arrays permiten acceder a cualquier dato en cualquier posición en tiempo constante, lo que los hace muy eficientes para ciertas operaciones.
  • Algoritmos de ordenación y búsqueda: Muchos algoritmos requieren el uso de arrays para funcionar correctamente.

Linked list (Listas enlazadas)

Los arrays almacenan elementos en ubicaciones de memoria contiguas, lo que resulta en direcciones fácilmente calculables para los elementos almacenados y permite un acceso más rápido a un elemento en un índice específico. Las listas enlazadas son menos rígidas en su estructura de almacenamiento, y generalmente los elementos no se almacenan en ubicaciones contiguas, por lo que necesitan ser almacenados con etiquetas adicionales que proporcionen una referencia al siguiente elemento. Esta diferencia en el esquema de almacenamiento de datos determina qué estructura de datos sería más adecuada para una situación dada.

La implementación de una lista enlazada puede variar dependiendo del lenguaje de programación. Aquí te dejo un ejemplo básico de cómo se podría implementar una lista enlazada en JavaScript:

// Definir la clase Nodo
class Node {
  constructor(data) {
    this.data = data;
    this.next = null;
  }
}

// Definir la clase ListaEnlazada
class LinkedList {
  constructor() {
    this.head = null;
  }

  // Método para agregar un nuevo nodo al final de la lista
  append(data) {
    const newNode = new Node(data);

    if (!this.head) {
      this.head = newNode;
      return;
    }

    let current = this.head;
    while (current.next) {
      current = current.next;
    }

    current.next = newNode;
  }

  // Método para imprimir la lista
  print() {
    let current = this.head;
    while (current) {
      console.log(current.data);
      current = current.next;
    }
  }
}

// Ejemplo de uso
const listaEnlazada = new LinkedList();
listaEnlazada.append(1);
listaEnlazada.append(2);
listaEnlazada.append(3);

listaEnlazada.print();

En este ejemplo, la clase Node representa un nodo de la lista con un valor (data) y una referencia al siguiente nodo (next). La clase LinkedList tiene un puntero a la cabeza de la lista (head) y métodos para agregar nodos al final (append) e imprimir la lista (print).

Las listas enlazadas se utilizan en diversos contextos, como por ejemplo:

  1. Implementación de pilas y colas.
  2. Implementación de gráficos: la representación de gráficos de listas de adyacencia es la más popular, que utiliza una lista vinculada para almacenar vértices adyacentes.
  3. Asignación de memoria dinámica: se utiliza una lista enlazada de bloques libres.
  4. Mantenimiento del directorio de nombres.
  5. Realización de operaciones aritméticas con números enteros largos

Stack (Pila)

Una pila es una colección lineal de elementos donde los elementos se insertan y se eliminan en un orden específico. También se llama una Estructura de Datos LIFO (Last In, First Out) porque sigue el principio “último en entrar, primero en salir”, es decir, el elemento que se inserta en último lugar es el primero en ser retirado.

Aquí te dejo un ejemplo básico de cómo se podría implementar una pila en JavaScript:

class Stack {
    constructor() {
        this.items = [];
    }

    // Agrega un elemento a la pila
    push(element) {
        this.items.push(element);
    }

    // Elimina un elemento de la pila
    pop() {
        if (this.items.length == 0)
            return "Underflow";
        return this.items.pop();
    }

    // Devuelve el elemento superior de la pila
    peek() {
        return this.items[this.items.length - 1];
    }

    // Verifica si la pila está vacía
    isEmpty() {
        return this.items.length == 0;
    }

    // Imprime los elementos de la pila
    printStack() {
        var str = "";
        for (var i = 0; i < this.items.length; i++)
            str += this.items[i] + " ";
        return str;
    }
}

// Usando la pila
var stack = new Stack();

console.log(stack.isEmpty()); // devuelve true

stack.push(10);
stack.push(20);
stack.push(30);

console.log(stack.printStack()); // imprime 10 20 30
console.log(stack.peek()); // imprime 30

stack.pop();
console.log(stack.printStack()); // imprime 10 20

En este código, la clase Stack tiene métodos para agregar un elemento a la pila (push), eliminar un elemento de la pila (pop), ver el elemento superior de la pila (peek), verificar si la pila está vacía (isEmpty) e imprimir los elementos de la pila (printStack).

Las pilas se utilizan en diversos contextos, como por ejemplo:

  1. Para evaluar expresiones con operandos y operaciones.
  2. En el historial de navegación web, donde cada nueva página visitada se añade a la pila y podemos retroceder en el historial.
  3. En compiladores, sistemas operativos y programas de aplicaciones, para la organización de la memoria.
  4. Para la evaluación de expresiones aritméticas en notación postfija.
  5. En la implementación de funciones de deshacer en editores de texto.

Queue (Cola)

Una cola es una colección lineal de elementos donde los elementos se insertan y se eliminan en un orden particular. La cola también se llama una Estructura de Datos FIFO (First In, First Out) porque sigue el principio “primero en entrar, primero en salir”, es decir, el elemento que se inserta primero es el primero en ser retirado.

Aquí te dejo un ejemplo básico de cómo se podría implementar una cola en JavaScript:

class Queue {
    constructor() {
        this.items = [];
    }

    // Agrega un elemento al final de la cola
    enqueue(element) {
        this.items.push(element);
    }

    // Elimina un elemento del frente de la cola
    dequeue() {
        if(this.isEmpty())
            return "Underflow";
        return this.items.shift();
    }

    // Devuelve el elemento del frente de la cola
    front() {
        if(this.isEmpty())
            return "No elements in Queue";
        return this.items[0];
    }

    // Verifica si la cola está vacía
    isEmpty() {
        return this.items.length == 0;
    }

    // Imprime los elementos de la cola
    printQueue() {
        var str = "";
        for(var i = 0; i < this.items.length; i++)
            str += this.items[i] +" ";
        return str;
    }
}

// Usando la cola
var queue = new Queue();

console.log(queue.isEmpty()); // devuelve true

queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);

console.log(queue.printQueue()); // imprime 10 20 30
console.log(queue.front()); // imprime 10

queue.dequeue();
console.log(queue.printQueue()); // imprime 20 30

En este caso, Queue es una clase que representa una cola. Los elementos se agregan al inicio de la lista y se quitan desde el final, siguiendo el principio FIFO.

Las colas se utilizan en diversos contextos, como por ejemplo:

  1. En sistemas de atención al cliente, donde cada nuevo cliente se añade al final de la cola y se atiende en el orden en que llegó.
  2. En la gestión de operaciones, para analizar y optimizar diferentes aspectos relacionados con el flujo de personas o productos en un sistema.
  3. En la logística y el transporte, para diseñar rutas y horarios eficientes, considerando el tiempo de espera en los puntos de carga y descarga.
  4. En la gestión de inventarios, permitiendo determinar los niveles óptimos de stock y reordenamiento.

Hash Table

Hash Table, Map, HashMap, Dictionary y Asociative son todos nombres para la misma estructura de datos. Es una de las estructuras de datos más comúnmente utilizadas.

Es una estructura de datos que implementa el tipo de dato abstracto llamado diccionario. Esta asocia llaves o claves con valores. La operación principal que soporta de manera eficiente es la búsqueda: permite el acceso a los elementos almacenados a partir de una clave generada. Funciona transformando la clave con una función hash en un hash, un número que identifica la posición donde la tabla hash localiza el valor deseado.

Las tablas hash se suelen implementar sobre vectores de una dimensión, aunque se pueden hacer implementaciones multi-dimensionales basadas en varias claves. Aquí te dejo un ejemplo básico de cómo se podría implementar una tabla hash en JavaScript:

class HashTable {
    constructor() {
        this.table = {};
    }

    // Agrega un elemento a la tabla hash
    put(key, value) {
        this.table[key] = value;
    }

    // Obtiene un elemento de la tabla hash
    get(key) {
        return this.table[key];
    }

    // Elimina un elemento de la tabla hash
    remove(key) {
        delete this.table[key];
    }

    // Imprime los elementos de la tabla hash
    printTable() {
        for (let key in this.table) {
            if (this.table.hasOwnProperty(key)) {
                console.log(key + " -> " + this.table[key]);
            }
        }
    }
}

// Usando la tabla hash
var hashTable = new HashTable();

hashTable.put("name", "John");
hashTable.put("age", 30);
hashTable.put("city", "New York");

hashTable.printTable(); // imprime name -> John, age -> 30, city -> New York
console.log(hashTable.get("name")); // imprime John

hashTable.remove("name");
hashTable.printTable(); // imprime age -> 30, city -> New York

En este código, la clase HashTable tiene métodos para agregar un elemento a la tabla hash (put), obtener un elemento de la tabla hash (get), eliminar un elemento de la tabla hash (remove) e imprimir los elementos de la tabla hash (printTable).

Las tablas hash se utilizan en diversos contextos, como por ejemplo:

  1. En bases de datos para la indexación.
  2. En estructuras de datos basadas en disco.
  3. En algunos lenguajes de programación como Python y JavaScript, se usa para implementar objetos.
  4. Para el mapeo de caché para un acceso rápido a los datos.
  5. Para la verificación de contraseña.
  6. Se usa en criptografía como un resumen de mensaje.

Tree (Árbol)

Un árbol es una estructura de datos que simula una estructura de árbol jerárquica, con un valor raíz y subárboles de hijos con un nodo padre.

Se define de forma recursiva como una colección de nodos, empezando por un nodo raíz, donde cada nodo es una estructura de datos que contiene un valor, y opcionalmente una lista de referencias a otros nodos (sus hijos), con la limitación de que ninguna referencia esté duplicada, y que ninguna apunte al nodo raíz.

Los árboles se utilizan en diversos contextos, como por ejemplo:

  1. En la representación de jerarquías.
  2. En la estructura del DOM (Document Object Model) en desarrollo web.
  3. En algoritmos de aprendizaje supervisado no paramétrico, como los árboles de decisión.
  4. En la representación de grafos acíclicos dirigidos y mínimamente conectados.

Binary Tree (Árbol Binario)

Un árbol binario es una estructura de datos en forma de árbol en la que cada nodo puede tener como máximo dos hijos, conocidos como el hijo izquierdo y el hijo derecho.

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

class BinaryTree {
    constructor() {
        this.root = null;
    }

    // Agrega un nodo al árbol binario
    add(data) {
        const newNode = new Node(data);

        if (this.root === null) {
            this.root = newNode;
        } else {
            this.insertNode(this.root, newNode);
        }
    }

    // Inserta un nodo en el árbol binario
    insertNode(node, newNode) {
        if (newNode.data < node.data) {
            if (node.left === null) {
                node.left = newNode;
            } else {
                this.insertNode(node.left, newNode);
            }
        } else {
            if (node.right === null) {
                node.right = newNode;
            } else {
                this.insertNode(node.right, newNode);
            }
        }
    }

    // Recorre el árbol binario en orden
    inorder(node) {
        if (node !== null) {
            this.inorder(node.left);
            console.log(node.data);
            this.inorder(node.right);
        }
    }
}

// Usando el árbol binario
const BT = new BinaryTree();

BT.add(15);
BT.add(25);
BT.add(10);
BT.add(7);
BT.add(22);
BT.add(17);
BT.add(13);
BT.add(5);
BT.add(9);
BT.add(27);

BT.inorder(BT.root); // imprime los nodos en orden

En este código, la clase Node representa un nodo en el árbol binario. Cada nodo tiene un data que almacena el valor del nodo, un left que es el nodo hijo izquierdo y un right que es el nodo hijo derecho.

La clase BinaryTree representa el árbol binario. Tiene un root que es el nodo raíz del árbol. También tiene métodos para agregar un nodo al árbol (add), insertar un nodo en el árbol (insertNode), y recorrer el árbol en orden (inorder).

Eliminar un nodo en un árbol binario de búsqueda en JavaScript puede ser un poco complicado porque hay varias situaciones que debes considerar:

  • El nodo a eliminar es una hoja (no tiene hijos).
  • El nodo a eliminar tiene un solo hijo.
  • El nodo a eliminar tiene dos hijos.

Aquí te muestro cómo puedes hacerlo:

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

class BinaryTree {
    constructor() {
        this.root = null;
    }

    // ... otros métodos ...

    // Elimina un nodo del árbol binario
    remove(data) {
        this.root = this.removeNode(this.root, data);
    }

    // Elimina un nodo del árbol binario
    removeNode(node, key) {
        if (node === null) {
            return null;
        } else if (key < node.data) {
            node.left = this.removeNode(node.left, key);
            return node;
        } else if (key > node.data) {
            node.right = this.removeNode(node.right, key);
            return node;
        } else {
            if (node.left === null && node.right === null) {
                node = null;
                return node;
            }

            if (node.left === null) {
                node = node.right;
                return node;
            } else if (node.right === null) {
                node = node.left;
                return node;
            }

            let aux = this.findMinNode(node.right);
            node.data = aux.data;

            node.right = this.removeNode(node.right, aux.data);
            return node;
        }
    }

    // Encuentra el nodo con el valor mínimo
    findMinNode(node) {
        if (node.left === null)
            return node;
        else
            return this.findMinNode(node.left);
    }
}

// Usando el árbol binario
const BT = new BinaryTree();

BT.add(15);
BT.add(25);
BT.add(10);
BT.add(7);
BT.add(22);
BT.add(17);
BT.add(13);
BT.add(5);
BT.add(9);
BT.add(27);

BT.remove(5);
BT.inorder(BT.root); // imprime los nodos en orden

En este código, la clase BinaryTree tiene un método remove que elimina un nodo del árbol. Este método llama a removeNode, que es un método recursivo que busca el nodo a eliminar y lo elimina de acuerdo a las reglas mencionadas anteriormente. Si el nodo a eliminar tiene dos hijos, se busca el nodo con el valor mínimo en el subárbol derecho (usando findMinNode), se copia su valor al nodo a eliminar y luego se elimina el nodo con el valor mínimo.

Binary Search Tree (Árbol de búsqueda binaria)

Un árbol de búsqueda binaria, también llamado árbol binario ordenado o clasificado, es una estructura de datos de árbol binario con raíz, donde la clave de cada nodo interno es mayor que todas las claves en el subárbol izquierdo respectivo y menor que las claves en el subárbol derecho.

Full Binary Tree (Árbol binario propio)

Un árbol binario propio es un tipo especial de árbol binario en el que cada nodo padre o nodo interno tiene ya sea dos o ningún hijo. También se conoce como un árbol binario propio.

Árbol binario propio
Árbol binario propio


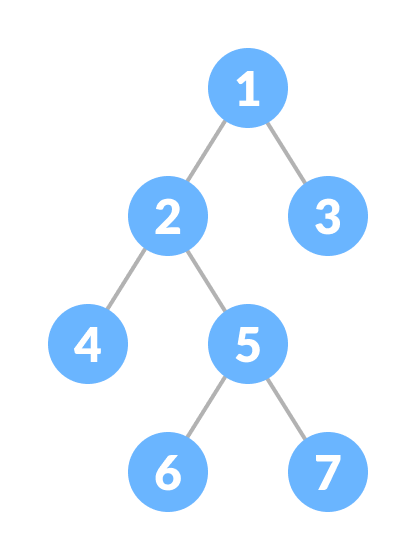
Complete Binary Tree (Árbol binario completo)

Un árbol binario completo es un árbol binario en el que todos los niveles están completamente llenos, excepto posiblemente el más bajo, que se llena desde la izquierda.

Un árbol binario completo es similar a un árbol binario propio, pero con dos diferencias importantes:

  1. Todos los elementos hoja deben inclinarse hacia la izquierda.
  2. El último elemento hoja puede no tener un hermano derecho, es decir, un árbol binario completo no tiene que ser un árbol binario propio.
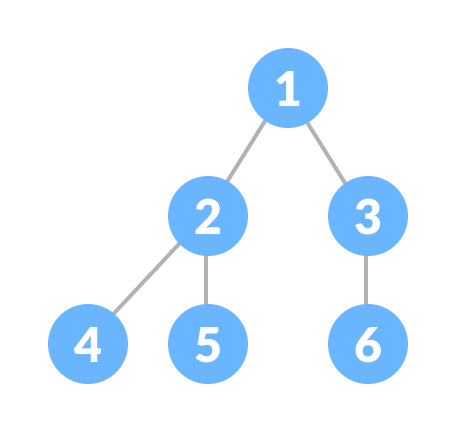
Árbol binario completo
Árbol binario completo


Balanced Tree (Árbol binario equilibrado)

Un árbol binario equilibrado, también conocido como árbol binario balanceado en altura, se define como un árbol binario en el que la diferencia de altura entre el subárbol izquierdo y el subárbol derecho de cualquier nodo no es mayor que 1.

Aquí te muestro cómo puedes implementar un árbol AVL en JavaScript:

class Node {
    constructor(data, left = null, right = null) {
        this.data = data;
        this.left = left;
        this.right = right;
        this.height = 1;
    }
}

class AVLTree {
    constructor() {
        this.root = null;
    }

    getHeight(node) {
        if (node === null) {
            return 0;
        }
        return node.height;
    }

    getBalance(node) {
        if (node === null) {
            return 0;
        }
        return this.getHeight(node.left) - this.getHeight(node.right);
    }

    leftRotate(node) {
        let rightNode = node.right;
        let rightLeftNode = rightNode.left;

        rightNode.left = node;
        node.right = rightLeftNode;

        node.height = Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1;
        rightNode.height = Math.max(this.getHeight(rightNode.left), this.getHeight(rightNode.right)) + 1;

        return rightNode;
    }

    rightRotate(node) {
        let leftNode = node.left;
        let leftRightNode = leftNode.right;

        leftNode.right = node;
        node.left = leftRightNode;

        node.height = Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1;
        leftNode.height = Math.max(this.getHeight(leftNode.left), this.getHeight(leftNode.right)) + 1;

        return leftNode;
    }

    insert(data) {
        this.root = this.insertNode(this.root, data);
    }

    insertNode(node, data) {
        if (node === null) {
            return new Node(data);
        } else if (data < node.data) {
            node.left = this.insertNode(node.left, data);
        } else if (data > node.data) {
            node.right = this.insertNode(node.right, data);
        } else {
            return node;
        }

        node.height = 1 + Math.max(this.getHeight(node.left), this.getHeight(node.right));

        let balance = this.getBalance(node);

        if (balance > 1 && data < node.left.data) {
            return this.rightRotate(node);
        }

        if (balance < -1 && data > node.right.data) {
            return this.leftRotate(node);
        }

        if (balance > 1 && data > node.left.data) {
            node.left = this.leftRotate(node.left);
            return this.rightRotate(node);
        }

        if (balance < -1 && data < node.right.data) {
            node.right = this.rightRotate(node.right);
            return this.leftRotate(node);
        }

        return node;
    }
}

// Usando el árbol AVL
let avlTree = new AVLTree();
avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(30);
avlTree.insert(40);
avlTree.insert(50);
avlTree.insert(25);

En este código, la clase Node representa un nodo en el árbol AVL. Cada nodo tiene un data que almacena el valor del nodo, un left que es el nodo hijo izquierdo, un right que es el nodo hijo derecho, y una height que es la altura del nodo.

La clase AVLTree representa el árbol AVL. Tiene un root que es el nodo raíz del árbol. También tiene métodos para obtener la altura de un nodo (getHeight), obtener el factor de equilibrio de un nodo (getBalance), rotar un nodo a la izquierda (leftRotate), rotar un nodo a la derecha (rightRotate), e insertar un nodo en el árbol (insert). El método insert llama a insertNode, que es un método recursivo que inserta un nodo en el árbol y luego equilibra el árbol.

Unbalanced Tree (Árbol binario desequilibrado)

Un árbol binario desequilibrado es aquel que no cumple con las condiciones de equilibrio, es decir, la diferencia de altura entre el subárbol izquierdo y el subárbol derecho de al menos un nodo es mayor que 1. Esto puede resultar en un rendimiento subóptimo en términos de tiempo de búsqueda y otras operaciones en comparación con árboles balanceados.

Graph (Grafo)

Los grafos en estructuras de datos son estructuras de datos no lineales compuestas por un número finito de nodos o vértices y las aristas que los conectan. Los grafos en estructuras de datos se utilizan para abordar problemas del mundo real en los que representan el área del problema como una red, como en redes telefónicas, redes de circuitos y redes sociales.

Directed Graph (Grafo dirigido)

Un grafo dirigido es un conjunto de objetos (llamados vértices o nodos) que están conectados entre sí, donde todas las aristas están dirigidas desde un vértice hacia otro. A veces, a un grafo dirigido se le llama grafo dirigido (digraph) o red dirigida. En contraste, un grafo donde las aristas son bidireccionales se llama grafo no dirigido.

Undirected Graph (Grafo no dirigido)

Un grafo no dirigido es un conjunto de objetos (llamados vértices o nodos) que están conectados entre sí, donde todas las aristas son bidireccionales. A veces, a un grafo no dirigido se le llama red no dirigida. En contraste, un grafo donde las aristas tienen una dirección se llama grafo dirigido.

Spanning Tree (Árbol de expansión)

Un árbol de expansión (o spanning tree) es un subconjunto del grafo G que abarca todos los vértices con el número mínimo posible de aristas. Por lo tanto, un árbol de expansión no tiene ciclos y no puede estar desconectado.

Graph Representation (Representación de grafo)

Un grafo puede representarse ya sea como una matriz de adyacencia o como una lista de adyacencia.

La matriz de adyacencia es una matriz 2D de tamaño V x V, donde V es el número de vértices en un grafo. Si la ranura adj[i][j] es igual a 1, indica que hay una arista desde el vértice i hacia el vértice j.

La lista de adyacencia es un array de vectores, y su tamaño es igual al número de vértices. Si la entrada array[i] representa la lista de vértices adyacentes al vértice i. Esta representación también puede usarse para representar un grafo ponderado, donde los pesos de las aristas se pueden representar como listas de pares.

Ventajas de la matriz de adyacencia:

  • Las operaciones básicas, como agregar una arista, eliminar una arista y verificar si hay una arista del vértice i al vértice j, son extremadamente eficientes en tiempo, operaciones de tiempo constante.
  • Si el grafo es denso y el número de aristas es grande, una matriz de adyacencia debería ser la primera elección. Incluso si el grafo y la matriz de adyacencia son dispersos, podemos representarlo utilizando estructuras de datos para matrices dispersas.
  • Sin embargo, la mayor ventaja proviene del uso de matrices. Los avances recientes en hardware nos permiten realizar incluso operaciones de matriz costosas en la GPU.
  • Al realizar operaciones en la matriz adyacente, podemos obtener ideas importantes sobre la naturaleza del grafo y la relación entre sus vértices.

Desventajas de la matriz de adyacencia:

  • El requisito de espacio VxV de la matriz de adyacencia la convierte en un devorador de memoria. Los grafos en la vida real generalmente no tienen demasiadas conexiones, y esta es la razón principal por la cual las listas de adyacencia son la mejor elección para la mayoría de las tareas.
  • Aunque las operaciones básicas son sencillas, operaciones como inEdges y outEdges son costosas cuando se utiliza la representación de matriz de adyacencia.

Ventajas de la lista de adyacencia:

  • Una lista de adyacencia es eficiente en cuanto a almacenamiento porque solo necesitamos almacenar los valores de las aristas. Para un grafo disperso con millones de vértices y aristas, esto puede significar un ahorro considerable de espacio.
  • También ayuda a encontrar fácilmente todos los vértices adyacentes a un vértice específico.

Desventajas de la lista de adyacencia:

  • Encontrar la lista de adyacencia no es más rápido que la matriz de adyacencia, ya que primero se deben explorar todos los nodos conectados para encontrarlos.

  • Wiki - Matriz

  • Wiki - Lista

Heap (Montículo)

Un montículo (Heap) es una estructura de datos basada en árboles que sigue las propiedades de un árbol binario completo y puede ser un Min Heap (montículo mínimo) o un Max Heap (montículo máximo).

  • Min Heap: En un Min Heap, el valor de cada nodo es menor o igual que los valores de sus hijos, lo que significa que el nodo con el valor mínimo se encuentra en la raíz del montículo.
  • Max Heap: En un Max Heap, el valor de cada nodo es mayor o igual que los valores de sus hijos, y el nodo con el valor máximo está en la raíz del montículo.

Los montículos se utilizan comúnmente para implementar colas de prioridad, algoritmos de ordenamiento eficientes como HeapSort y en diversas aplicaciones donde se requiere acceso eficiente al elemento extremo (mínimo o máximo) del conjunto de datos.

‹ ›